MATRIKS KELAS 11

 KHIRQA ADAVYA (19)

XI IPS 3

 Matriks

Pengertian Matriks

Macam-macam Matriks

Operasi Matriks

Contoh Soal Matriks

A. PENGERTIAN MATRIKS

Menurut Wikipedia Matriks adalah susunan, bilangan, simbol, atau ekspresi, yang disusun dalam baris dan kolom sehingga membentuk suatu bangun persegi. Beberapa hal yang perlu kita ketahui yaitu notasi pada matriks harus huruf kapital sedangkan unsur-unsur atau elemennya harus huruf kecil. Suatu matriks biasa ditulis didalam tanda kurung lengkung "( )" atau kurung siku "[ ]".

Matriks merupakan kumpulan bilangan, simbol atau ekspresi berbentuk persegi panjang yang disusun menurut baris dan kolom. Bilangan-bilangan yang terdapat pada suatu matriks disebut dengan elemen atau disebut juga anggota dari suatu matriks.

Matriks didefinisikan sebagai sekelompok bilangan di dalam sebuah jajaran berbentuk persegi panjang yang diatur berdasarkan baris dan kolom serta terletak di antara dua tanda kurung. Fungsi tanda kurung adalah untuk mengapit susunan anggota matriks. Bentuk tanda kurung bisa berupa kurung biasa maupun kurung siku. Bilangan pada matriks disebut unsur atau elemen matriks. Berdasarkan susunannya, kumpulan elemen matriks dibedakan menjadi dua macam, yaitu

• baris: kumpulan elemen matriks yang tersusun secara mendatar (horizontal)
• kolom: kumpulan elemen matriks yang tersusun secara tegak (vertikal).

Selain baris dan kolom, di dalam matriks, dikenal juga istilah ‘ordo’. Ordo matriks adalah bilangan yang menunjukkan jumlah baris (m) dan kolom (n) yang ada pada matriks tersebut. Sebuah matriks biasanya ditulis menggunakan huruf kapital dan tebal. Matriks yang mempunyai m baris dan n kolom disebut dengan matrik m x n dan dinamakan matriks dengan ordo m x n.

B. MACAM-MACAM MATRIKS

1. Matriks Transpos

Matriks transpos ialah matriks yang menukar baris menjadi kolom dan kolom menjadi baris. Matriks transpos biasa dilambangkan dengan t. Contohnya matriks A berikut :

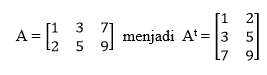
2. Matriks Simetri

Matriks simetri ialah suatu matriks dimana matriks transposnya memiliki unsur elemen yang sama. Contohnya sebagai berikut :

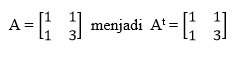
3. Matriks Persegi

Matriks persegi ialah suatu matriks yang memiliki ordo yang sama. Contohnya matriks A ordo 2x2 dan B ordo 3x3 berikut :

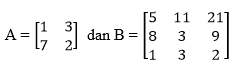
4. Matriks Segitiga Atas dan Bawah

Matriks segitiga atas ialah matriks dimana unsur atau elemen dibawah diagonal utamanya bernilai 0. Contohnya sebagai berikut :

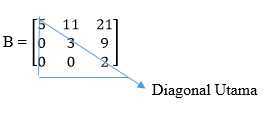
Sedangkan matriks segitiga bawah merupakan kebalikan dari matrik atas dimana, diatas diagonal utamanya selalu bernilai 0. Contohnya sebagai berikut :

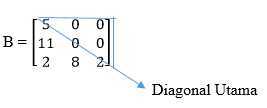
5. Matriks Diagonal

Matriks diagonal ialah matriks dimana unsur selain diagonal utamanya bernilai 0. Contohnya sebagai berikut :

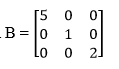
6. Matriks Identitas

Matriks identitas ialah matriks yang diagonal utamanya selalu bernilai 1. Contohnya sebagai berikut :

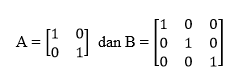
7. Matriks Baris

Matriks baris adalah matriks yang hanya memiliki satu baris dan biasanya berordo 1 x n. Contohnya sebagai berikut :

 

8. Matriks Kolom

Matriks kolom adalah matriks yang hanya terdiri dari satu kolom sehingga disebut matriks berordo m x 1. Contohnya sebagai berikut :

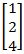
9. Matriks Skalar

Matriks skalar adalah matriks yang diagonal utamanya terdiri dari elemen yang sama, sedangkan elemen lainnya adalah nol. Contohnya sebagai berikut :

10. Matriks Nol

Matriks nol adalah matriks yang semua elemen pada matriks adalah bilangan nol.

C. OPERASI MATRIKS

1. Penjumlahan Matriks

Syarat pada penjumlahan matriks ialah harus memiliki ordo yang sama, dan menambahkan pada posisi atau letak yang sama. Contohnya sebagai berikut :

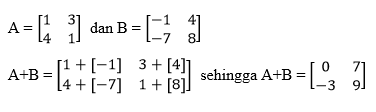
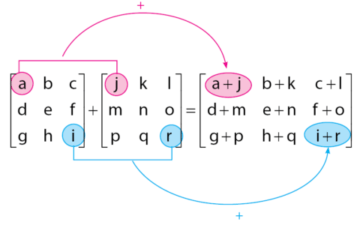
2. Pengurangan Matriks

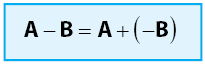
Syarat pada pengurangan matriks juga sama dengan penjumlahan. Misal matriks C adalah pengurangan matriks A dan B, perlu kita ketahui bahwa matriks pengurangan ialah sama dengan penambahan Matriks A dengan perkalian skalar -1 dengan matriks B.

"C=A-B" sama dengan "C = A+ [-1] B"

Contoh pengurangan matriks sebagai berikut :

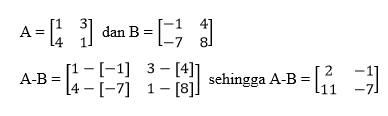
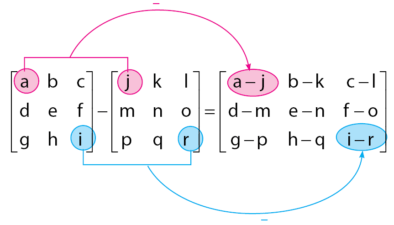
3. Perkalian Matriks

• Perkalian Matriks dengan Skalar

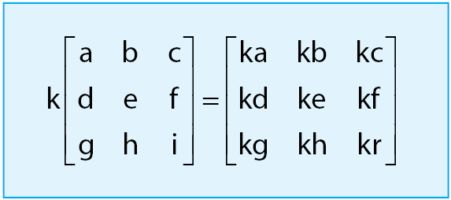
Pada perkalian matriks dengan skalar caranya yaitu mengalikan nilai skalar dengan semua letak matriks. Contohnya sebagai berikut :

• Perkalian Matriks dengan Matriks

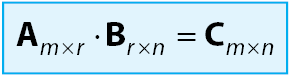
Syarat pada perkalian matriks ialah jumlah kolom pada matriks pertama sama dengan jumlah baris pada matriks kedua. Contohnya sebagai berikut perkalian A2x3 dan 3x3 :

E. CONTOH SOAL MATRIKS

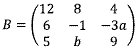
1. Diketahui matriks   dan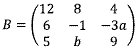

    

Jika A = B, maka a + b + c =….

A. − 7

B. − 5

C. − 1

D. 5

E. 7

Pembahasan :

Kesamaan dua matriks:

4a = 12

a = 3

3a = − 3b

−3a = − 3b

−3(3) = − 3b

−9 = − 3b

b = 3

3c = b

3c = 3

c =  1

a + b + c = 3 + ( 3) + ( 1) = 7

2. Diketahui matriks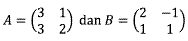 

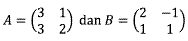
Memenuhi AX = B, tentukan matriks X

Pembahasan :

Jika AX = B, maka untuk mencari X adalah

X = A−1 B

Cari invers matriks A terlebih dahulu, setelah ketemu kalikan dengan matriks B

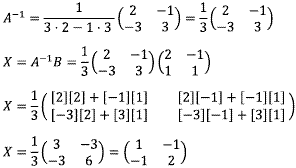
AX = B maka X = A−1 B

XA = B  maka X = B A−1

F. DAFTAR PUSTAKA

• http://rumus-matematika.com/materi-matriks-lengkap-dan-contohnya/
• https://www.materipelajaran.web.id/2018/01/pengertian-matriks-jenis-dan-operasi-matriks.html
• https://www.belajarmtk.com/pengertian-matriks-dan-macam-macam-matriks/
• https://matematikauniversitas.blogspot.com/2013/03/macam-macam-matriks.html
• https://idschool.net/sma/operasi-hitung-penjumlahan-pengurangan-perkalian-matriks/
• https://contoh123.info/51-contoh-soal-dan-pembahasan-operasi-matriks/