SOAL TRIGONOMETRI DAN REMEDIAL PAT
KHIRQA ADAVYA (19)
X IPS 3
TUGAS MTK DAN REMEDIAL PAT
(LETAK REMEDIAL ADA DI BAWAH TUGAS DITANDAI DENGAN JUDUL)
Segitiga sama kaki dengan sudut lan cip C
memiliki panjang BC: 12 berapa panjang AB?
Pada
suatu segitiga dengan sisi-sisi a, b, dan c memenuh a²-b²= c²-bc. Maka besar sudut A adalah ….
2. Menyelesaikan membaca gambar fungsi trigonometri f(x) = sin x, f(x) = cos x, f(x) = tan x, f(x) = csc x, f(x) = sec x, f(x) = cot x
Soal 1 :
3. Menyelesaikan range nilai fungsi trigonometri f(x) = sin x, f(x) = cos x, f(x) = tan x, f(x) = csc x, f(x) = sec x, f(x) = cot x
Soal 1 :
4. Menyelesaikan fungsi trigonometri dengan menggunakan lingkaran satuan untuk menentukan periode maksimum dan minimum
Sudut yang terbentuk searah dengan jarum jam, sehingga tandanya negatif, yakni .Karena satu putaran sama dengan , maka sama dengan
Perhatikan sketsa gambar berikut.
B.Himpunan penyelesaian persamaan
dengan
Dengan menggunakan bentuk umum rumus sudut ganda sinus, yaitu
diperoleh
Persamaan terakhir menunjukkan bahwa
atau
Jadi, HP persamaan trigonometri tersebut adalah
X IPS 3
TUGAS MTK DAN REMEDIAL PAT
(LETAK REMEDIAL ADA DI BAWAH TUGAS DITANDAI DENGAN JUDUL)
3.7
Menyelesaikan cara merubah satuan pengukuran sudut trigonometri radian ke
derajat, derajat ke radian
1
radian= 180°/π
Contoh:
Contoh
Soal 1
Soal:
Berapa derajatkah sudut 3,5 radian?
Jawab:
3,5
radian = 3,5 x(180°/π) = 200,535°
Contoh soal 2
Soal:
Hitunglah sudut 2,2 radian dalam derajat!
Jawab:
2,2
radian = 2,2 x (180°/π) = 126°
B . Derajat ke Radian
1°=(π/180) radian
Contoh
Soal 3
Soal:
15° berapa radian?
Jawab:
15°
= 15 x (π/180) = 0,265 radian
Contoh
Soal 4
Soal:
Nyatakan sudut 60° dalam π radian!
Jawab:
60°
= 60 x (π/180) = π/3 radian
3.7
Menyelesaikan rasio trigonometri (sinus, cosinus, tangen, cosecan, secan, dan
cotangen) pada segitiga siku-siku dan dudut istimewa (60° , 30° , 45° )
Sudut
istimewa adalah sudut yang perbandin gantrigonometrinya dapat dicari tanpa
memakai table matematika atau kalkulator, yaitu: 0°, 30°, 45°,60°, dan 90°.
Sudut-sudut
istimewa yang akan dipelajari adalah 30°, 45°,dan 60°.
Untuk
mencari nilai perbandingan trigonometri sudut istimewa digunakan segitiga
siku-siku seperti gambar berikut ini.
Contoh:
3.7
Menyelesaikan rasio trigonometri (sinus, cosinus, tangen, cosecan, secan, dan
cotangen) pada segitiga siku-siku di dalam koordinat kartesius
a.
sisi yang berhadapan dengan sudut adalah De atau depan
b.
sisi yang menempelnya di sudut siku2 adalah Sa atau Samping
c.sisi
yang berhadapan dengan sudut siku2 adalah Mi atau Miring
sin α
= de/mi csc α =
mi/de
cos
α= sa/mi sec α = mi/sa
tan
α = de/sa cot α = sa/de
segitiga siku2 ABC jika tan  = ¾ ( A sudut lancip)
brpkah cos
= ¾ ( A sudut lancip)
brpkah cos  ?
?
Diket:
tan α = ¾
Dit:
cos α?
Jwb:
carilah sisi miring dengan phytagoras
Yaitu
mi=5
cos
α = sa/mi = 4/5
3.8
Menyelesaikan rasio trigonometri untuk sudut-sudut di berbagai kuadran
sudut dapat dikelompokkan menjadi
4 wilayah atau kuadran didasarkan pada besarnya sudut, yaitu:
1. Sudut-sudut yang terletak di kuadran I,
yaitu sudut-sudut yang besarnya antara 0° sampai 900° atau 0° < 1a < 90°.
2. Sudut-sudut yang terletak di kuadran II,
yaitu sudut-sudut yang besarnya antara 90° sampai 180°
atau 90°
< 2a < 180°.
3. Sudut – sudut yang terletak di
kuadran III, yaitu sudut- sudut yang besarnya antara 180° < 3a < 270°.
4. Sudut – sudut yang terletak di
kuadran IV, yaitu sudut-sudut yang besarnya antara 270° < 3a < 360°
Untuk Kuadran I sin a
=y/r (positif) , cos a=x/
r (positif) , tan a= y/x
(positif)
Untuk Kuadran II sin a=
y/ r (positif) , cos a=
-x/ r (negatif) , tan a= y/ -x (negatif)
Untuk Kuadran III sin a=
-y /r (negatif) , cos a= -x/ r (negatif) ,tan a=-y/ -x (positif)
Untuk Kuadran IV sin a= –y/ r (negatif) , cos a x/ r (positif) = tan a –y/ x (negatif)
Hasil-hasil diatas, untuk
memudahkan dalam memahami dan menghafalkan
Diketahui cos β = ½ √3
Carilah : a. sin β b. tan β c.
sec β d. cosec β
Jawab: Karena tidak ada
keterangan, maka sudut terletak di kuadran I
BC² = AC²– AB² BC= √1
= 22 – (√3)2 = 1
= 4 - 3 = 1
Maka nilai dari
a. sin β = BC AC = ½
b. tan β = BC AB = 1 √3 . √3 √3 =
⅓ √3
c. sec β = AC AB = 2 √3 . √3 √3 = ⅔ √3
d. cosec β = AC BC = 2 1 = 2
3.8
Menyelesaikan persamaan trigonometri sederhana atau persamaan indentitas
trigonometri = rumus identitas trigonometri
1.
Rumus Jumlah Dan Selisih Dua Sudut
Rumus
Untuk Cosinus Jumlah Selisih Dua Sudut :
cos
(A + B) = cos A cos B – sin A sin B
cos
(A – B) = cos A cos B + sin A sin B
Rumus
Untuk Sinus Jumlah Dan Selisih Dua Sudut :
sin
(A + B) = sin A cos B + cos A sin B
sin
(A – B) = sin A cos B – cos A sin B
Rumus
Untuk Tangen Jumlah Dan Selisih Dua Sudut :
tan
A (A + B) = tan A + tan B/1 – tan A x tan B
tan
A (A – B) = tan A – tan B/1 + tan A x tan B
2.
Rumus Trigonometri Untuk Sudut Rangkap
Dengan
Menggunakan Rumus sin (A + B) Untuk A = B :
sin
2A = sin (A + B)
=
sin A cos A + cos A sin A
=
2 sin A cos A
Jadi,
sin 2A = 2 sin A cos A
Dengan
Menggunakan Rumus cos (A + B) Untuk A = B :
cos
2A = cos (A + A)
=
cos A cos A – sin A sin
=
cos 2A – sin 2A ……………(1)
=
cos 2A – (1 – cos 2A)
=
cos 2A – 1 + cos 2A
=
2 cos 2A – 1………………(2)
=
(1 – sin 2A) – sin 2A
=
1 – 2 sin 2A………………(3)-
Dari
Peramaan (1), (2), (3) diatas didapatkan rumus yaitu
Cos
2A = cos 2A – sin 2A
=
2 cos 2A – 1
=
1 – 2 sin 2A
Dengan
Menggunakan Rumus tan (A + B) Untuk A = B :
tan
2A = tan (A + A)
= tan A + tan A/1 tan A x tan A
= 2 tan A/1 – tan 2A
Jadi,
tan 2A = 2 tan A/1 – tan 2A
Contoh
Soal Identitas Trigonometri
Contoh
Soal :
Jika
tan 5°= p. Tentukan :
tan
50°
Penyelesaian
:]
tan
50° = tan (45° + 5°)
=
tan 45° + tan 5°/1 – tan 45° x tan 5°
=
1 + p/1 – p Jadi, hasilnya adalah = 1 + p/1 – p
3.8
Menyelesaikan Koordinat kutub ke koordinat kartesius, koordinat kartesius ke
koordinat kutub
Koordinat
kartesius suatu titik merupakan posisi suatu titik dalam arah sumbu x dan dalam
arah sumbu y terhadap titik asal O (0,0) sebagai titik pusatnya. Koordinat
kartesius ditulis dengan notasi titik P (x,y).
Koordinat
Kutub (Polar) suatu titik merupakan besarnya jarak suatu titik tertentu P (x,y)
terhadap titik asal O (0,0) dan besarnya sudut yang terbentuk oleh garis OP
terhadap sumbu x. Koordinat kutub ditulis dengan notasi P (r,α°).
P (x,y) ---->
P (r, α°)
α = tan^-1 (y/x) atau tan α =
y/x
Contoh:
Contoh
Soal Konversi Koordinat:
Penyelesaian:
Diketahui: x = 4 dan y = -3
maka
r = √x²+y² = √4²+(-3)² = √25 = 5
α = tan^-1 (y/x) = tan^-1 (-3/4)
= -36,69 ° atau -37°
Jadi
koordinat kutubnya (5, -37°).
Penyelesaian:
Diketahui: x = 6 dan y = 8
maka
r = √x²+y² = √6²+8² = √100 = 10
α = tan^-1 (y/x) = tan^-1 (8/6)
= 53,13 ° atau 53°
Jadi
koordinat kutubnya (10, 53°).
3.8
Menyelesaikan soal cerita perbandingan trigonometri
Seekor
kelinci yang berada di lubang tanah tempat persembunyiannya melihat seekor
elang yang sedang terbang dengan sudut
60∘. Jika jarak antara kelinci dan
elang adalah 18meter, maka tinggi elang dari atas tanah adalah⋯ meter.
Jwb:
sisi
depan sudut 60∘,
ditanyakan panjangnya dan sisi miring segitiga (hipotenusa) diketahui
panjangnya. Dengan demikian, perbandingan trigonometri yang dapat digunakan
adalah sinus
sin
60° = x/180
1/2√3 = 18
x=18. 1/2
=
9√3
3.9
Menyelesaikan aturan sinus diketahui 2 sudut dan 1 sisi
Aturan
Sinus (Law of Sines atau Sines Law/Rule) adalah teorema berupa persamaan yang
menghubungkan nilai sinus sudut dalam segitiga dengan panjang sisi di depannya
dalam bentuk perbandingan.
Diketahui
segitiga ABC dengan panjang sisi a: 4 cm
sudut a: 120° dan sudut b: 30° berapa panjang sisi c Karena jumlah besar
sudut dalam segitiga selalu 180∘,
maka ∠C=(180−120−30)∘=30∘. Selanjutnya, dengan menggunakan
Aturan Sinus, diperoleh
a/sin
A = c/sin C
4/sin
120° = c/sin 30°
4/√3
½ = c/ ½
C
= 4/√3= 4/3√3
3.9
Menyelesaikan aturan sinus diketahui 1 sudut dan 2 sisi
Diketahui
suatu taman di tengah kota berbentuk segitiga sembarang. Jika sudut apit
sebesar 60o dan dua sisi yang mengapitnya masing-masing panjangnya 18 meter dan
16 meter, maka luas taman tersebut adalah ….
Untuk
menentukan luas segitiga sembarang yang diketahui panjang dua sisi dan sudut
antara kedua sisi tersebut dapat memanfaatkan fungsi sinus.
L:
½ .18.16.sin 60°
L:
: ½ .18.16. ½ √3
L:
72√3 m²
3.9
Menyelesaikan aturan cos ditanya
sisi
Persamaan
pada aturan cosinus menyatakan hubungan antara kuadrat panjang sisi dengan
nilai cosinus dari salah satu sudut pada segitiga. Aturan cosinus dapat
digunakan untuk menentukan besar salah satu sudut segitiga saat tiga sisi
segitiha diketahui. Sedangkan untuk menentukan salah satu sisi segitiga, aturan
cosinus dapat digunakan saat diketahui dua sisi dan sudut apitnya.
Jwb:
c²
= a² + b² - 2ab cos 30°
c²
= 12² + 12² - 2(12) (12) (. ½ √3)
c²
= 2 (12²) - 12²√3
c=√12²(2-3)= 12√2-√3
3.9
Menyelesaikan aturan cos ditanya sudut
Jawab:
a²=b²+c²-bc
a²=
b² + c²-2bc. Cos A ÷ 2
0=
-bc + 2bc. Cos A
bc=
2bc.cos A
cos
A = bc/2bc
cos
A = ½ jdi A + 60°
3.7
Menyelesaikan sudut elevasi, sudut depresi
Dua
orang guru dengan tinggi badan yang sama yaitu 170 cm sedang berdiri memandang
puncak tiang bendera di sekolahnya. Guru pertama berdiri tepat 10 m di depan
guru kedua. Jika sudut elevasi guru pertama 60∘ dan guru kedua 30∘ maka dapatkah anda menghitung tinggi
tiang bendera tersebut?
Misalkan
panjang CD = BG = x
*).
Menentukan nilai x
Segitiga
ABG :
tan60∘=AB/x→AB=xtan60∘→AB= √3x
Segitiga
ABF , subsitusi ke AB= √3x
Tan
30° = AB/BF
1/√3
=√3x/ x+ 10
√3.√3x=
x+ 10
3x=
x+ 10
2x=10
x=5
AB
= √3x = √3. 5 = 5√3 jdi tinggi bendera
adalah 5√3
KD 3.10
1. Menyelesaikan gambar fungsi trigonometri f(x) = sin x, f(x) = cos x, f(x) = tan x, f(x) = csc x, f(x) = sec x, f(x) = cot x
Grafik di atas adalah grafik fungsi
) dengan bentuk umum .
Grafik juga menunjukkan bahwa nilai maksimum fungsinya , sedangkan nilai minimumnya , sehingga
Saat , nilai fungsinya , lalu berulang kembali di , sehingga periodenya . Dengan demikian, .
Jadi, grafik fungsi di atas adalah grafik fungsi
Grafik juga menunjukkan bahwa nilai maksimum fungsinya , sedangkan nilai minimumnya , sehingga
Saat , nilai fungsinya , lalu berulang kembali di , sehingga periodenya . Dengan demikian, .
Jadi, grafik fungsi di atas adalah grafik fungsi
2. Menyelesaikan membaca gambar fungsi trigonometri f(x) = sin x, f(x) = cos x, f(x) = tan x, f(x) = csc x, f(x) = sec x, f(x) = cot x
Soal 1 :
Pada interval 45°< x < 90° maka grafik dari y = 3 cos 2x akan
Diketahui:
y = 3 cos 2x
Ditanya: grafik y = 3 cos 2x pada interval 45° ≤ x ≤ 90°
Jawab:
Untuk menggambar grafik, diperlukan titik-titik yang melalui koordinat (x, y). Titik-titik tersebut diperoleh dengan cara mendaftar anggota pada grafik y = 3 cos 2x .
Karena hanya diperlukan pada interval 45° ≤ x ≤ 90° , maka kita hanya akan mendaftar sudut-sudut istimewa pada interval tersebut. Sudut istimewa diantara 45° - 90° adalah: 45°, 60°, dan 90°. Maka diperoleh:
x = 45°, 60°, dan 90°
subtitusikan nilai x satu persatu kedalam persamaan y
untuk x = 45°
y = 3 cos 2x
y = 3 cos 2(45°)
y = 3 cos 90°
y = 3(0)
y = 0
Maka diperoleh titik (45°, 0)
untuk x = 60°
y = 3 cos 2x
y = 3 cos 2(60°)
y = 3 cos 120°
Ingat! cos 120° terletak di kuadran II
y = 3 (-cos (180° - 60°))
y = 3
y =
Maka diperoleh titik (60°, )
untuk x = 90°
y = 3 cos 2x
y = 3 cos 2(90°)
y = 3 cos 180°
y = 3(-1)
y = -3
Maka diperoleh titik (90°, -3)
Dari titiik-titik tersebut kemudian digambar pada bidang kartesisus. Gambar grafik dapat dilihat pada lampiran. Dari grafik tersebut terlihat bahwa grafik y = 3 cos 2x terletak di bawah sumbu- x, atau pada sumbu- y negatif, dan graik tersebut juga terbuka ke atas.
∴ Jadi graik y = 3 cos 2x pada interval 45° ≤ x ≤ 90° akan terbuka keatas dan di bawah sumbu-x atau pada sumby-y negatif.
3. Menyelesaikan range nilai fungsi trigonometri f(x) = sin x, f(x) = cos x, f(x) = tan x, f(x) = csc x, f(x) = sec x, f(x) = cot x
Soal 1 :
Pada interval 0° < x < 90° grafik fungsi seluruhnya berada di atas sumbu x. fungsi tersebut adalah
Jawab:
y = sin 2* 0 = sin 0 = 0
y = sin 2 * 45 = sin 90 = 1
y = sin 2 * 90 = sin 180 = 0
jadi fungsi y = sin 2x
Soal 1 :
Nilai maksimum dari fungsi y = 4 sin x cos x adalah...
Jawab :
Nilai maksimum dari fungsi y = 4 sin x cos x adalah 2. Nilai dari sin ax dan cos ax adalah –1 ≤ sin ax ≤ 1 dan –1 ≤ cos ax ≤ 1, sehingga:
Nilai maksimum dari sin ax dan cos ax adalah 1
Nilai minimum dari sin ax dan cos ax adalah –1
dengan a adalah bilangan real
Rumus sudut rangkap pada trigonometri
sin 2A = 2 sin A cos A
cos 2A = cos² A – sin² A
cos 2A = 2 cos² A – 1
cos 2A = 1 – 2 sin² A
tan 2A = 
y = 4 sin x cos x
y = 2 . 2 sin x cos x
y = 2 . sin 2x
y = 2 sin 2x
karena nilai dari sin 2x adalah –1 ≤ sin 2x ≤ 1, maka y = 2 sin 2x akan bernilai maksimum jika sin 2x = 1
sehingga nilai maksimum dari y = 4 sin x cos x adalah
y = 2 sin 2x
y = 2 (1)
y = 2
Soal 2 :
Nilai minimum dari fungsi y = √3 cos x - sin x adalah...
Jawab :
Nilai Maksimum minimum fungsi trigonometri
y = √3 cos x - sin x ubah bentu ke y = k cos ( x - a)
a= √3
b = - 1
k = √(a²+b²)
k = √(3 +1)= +_2
Nilai minimum nya = -2
y = √3 cos x - sin x ubah bentu ke y = k cos ( x - a)
a= √3
b = - 1
k = √(a²+b²)
k = √(3 +1)= +_2
Nilai minimum nya = -2
Remedial PAT
1.Perbandingan Trigonometri

1.Perbandingan Trigonometri
A.Besar sudut yang sesuai dengan gambar di bawah adalah

Sudut yang terbentuk searah dengan jarum jam, sehingga tandanya negatif, yakni .Karena satu putaran sama dengan , maka sama dengan
Jadi, besar sudutnya adalah
2.Sudut Berelasi
A. Untuk perbandingan trigonometri berikut, nyatakanlah dalam perbandingan trigonometri sudut komplemennya
sin 20° Yaitu...
sin 20° = sin (90° − 70°)= cos 70°
B.Nyatakan tiap perbandingan trigonometri berikut di dalam sudut 37° !
tan 143° Yaitu...
Sudut 143° adapada kuadran II, hingga tan 143° memiliki nilai negatif.tan 143° = tan (180° − 37°)= -tan 37°
sin 20° = sin (90° − 70°)= cos 70°
B.Nyatakan tiap perbandingan trigonometri berikut di dalam sudut 37° !
tan 143° Yaitu...
Sudut 143° adapada kuadran II, hingga tan 143° memiliki nilai negatif.tan 143° = tan (180° − 37°)= -tan 37°
C.Untuk perbandingan trigonometri berikut, nyatakanlah dalam perbandingan trigonometri sudut komplemennya cos 53° yaitu..
cos 53° = cos (90° − 37°)= sin 37°
cos 53° = cos (90° − 37°)= sin 37°
D.Nyatakan tiap perbandingan trigonometri berikut di dalam sudut 37°
Sudut 233° ada pada kuadran III, sehingga sinus memiliki nilai negatif.
sin 233° = sin (270° − 37°)
= -cos 37°
Sudut 233° ada pada kuadran III, sehingga sinus memiliki nilai negatif.
sin 233° = sin (270° − 37°)
= -cos 37°
sin 233° = sin (270° − 37°)
= -cos 37°
3.Aturan Sinus Cosinus Dan Luas Segitiga
A.
Panjang sisi-sisi pada berbanding . Cosinus sudut yang terbesar dari segitiga tersebut adalah...
A.
Panjang sisi-sisi pada berbanding . Cosinus sudut yang terbesar dari segitiga tersebut adalah...
Perhatikan sketsa gambar berikut.
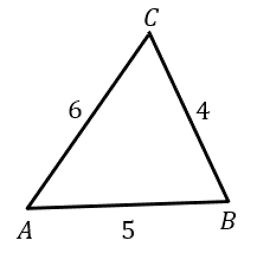
Kita misalkan , dan .
Dengan menggunakan Aturan Cosinus, nilai masing-masing cosinus sudut dapat ditentukan karena panjang ketiga sisi segitiganya telah diketahui.
Cosinus sudut adalah
Cosinus sudut adalah
Cosinus sudut adalah
Karena , maka cosinus sudut terbesar adalah pada sudut , Yaitu cos A =3/4
B. Sebuah mobil melaju dari tempat A sejauh km dengan arah , kemudian berbelok sejauh km ke tempat B dengan arah . Jarak A dan B adalah... km

Kita misalkan , dan .
Dengan menggunakan Aturan Cosinus, nilai masing-masing cosinus sudut dapat ditentukan karena panjang ketiga sisi segitiganya telah diketahui.
Cosinus sudut adalah
Cosinus sudut adalah
Cosinus sudut adalah
Karena , maka cosinus sudut terbesar adalah pada sudut , Yaitu cos A =3/4
Perhatikan sketsa gambar berikut.
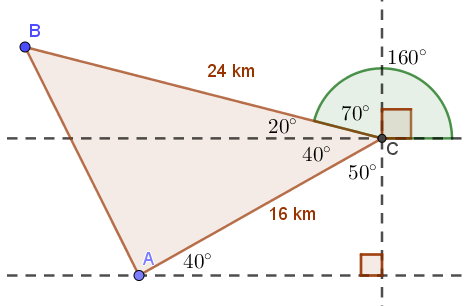
Pada segitiga di atas, diketahui , , dan . Dengan menggunakan Aturan Cosinus, diperoleh
Jadi, jarak A ke B adalah
C.d
dibuat segi- beraturan. Panjang sisi segi-12 beraturan tersebut adalah
Perhatikan sketsa gambar berikut.
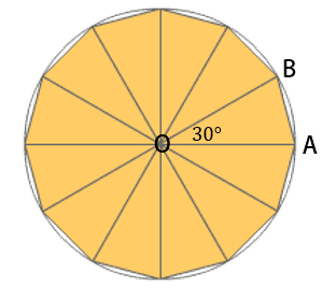
Pada segitiga , diketahui bahwa serta . Panjang sisi dapat dihitung dengan menggunakan Aturan Cosinus.
Jadi, panjang sisi segi- beraturan tersebut adalah

Pada segitiga , diketahui bahwa serta . Panjang sisi dapat dihitung dengan menggunakan Aturan Cosinus.
Jadi, panjang sisi segi- beraturan tersebut adalah
D.
Perhatikan sketsa segitiga berikut.
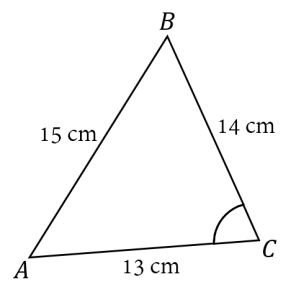
Karena ketiga panjang sisi segitiga diketahui, maka kita dapat mencari nilai terlebih dahulu dengan menggunakan Aturan Cosinus.
Panjang sisi samping .
Panjang sisi miring .
Panjang sisi depan .
Dengan demikian,

Karena ketiga panjang sisi segitiga diketahui, maka kita dapat mencari nilai terlebih dahulu dengan menggunakan Aturan Cosinus.
Panjang sisi samping .
Panjang sisi miring .
Panjang sisi depan .
Dengan demikian,
4. Persamaan Trigonometri
A. Himpunan penyelesaian persamaan untuk adalah ...
Diketahui:
Kemungkinan 1:
Untuk , diperoleh
Untuk , diperoleh
Kemungkinan 2:
Untuk , diperoleh
Untuk , diperoleh Jadi, himpunan penyelesaian persamaan trigonometri tersebut adalah
A.
Kemungkinan 1:
Untuk , diperoleh
Untuk , diperoleh
Kemungkinan 2:
Untuk , diperoleh
Untuk , diperoleh Jadi, himpunan penyelesaian persamaan trigonometri tersebut adalah
dengan
Dengan menggunakan bentuk umum rumus sudut ganda sinus, yaitu
diperoleh
Persamaan terakhir menunjukkan bahwa
atau
Jadi, HP persamaan trigonometri tersebut adalah
C.Jika diketahui
, maka himpunan penyelesaian untuk nilai pada interval adalah Hubungan sinus dan cosinus pada kuadran I dinyatakan oleh:
Oleh karena itu, persamaan dapat ditulis menjadi
Selanjutnya, dengan menggunakan konsep persamaan dasar trigonometri untuk cosinus, kita peroleh dua kemungkinan untuk mencari penyelesaian persamaan tersebut.
Kemungkinan 1:
Untuk nilai tertentu, kita peroleh nilai .
Catatan: Nilai yang diperoleh dianggap memenuhi bila dalam interval .
Kemungkinan 2:
Untuk nilai tertentu, kita peroleh nilai .
Jadi, himpunan penyelesaian untuk nilai adalah .
Oleh karena itu, persamaan dapat ditulis menjadi
Selanjutnya, dengan menggunakan konsep persamaan dasar trigonometri untuk cosinus, kita peroleh dua kemungkinan untuk mencari penyelesaian persamaan tersebut.
Kemungkinan 1:
Untuk nilai tertentu, kita peroleh nilai .
Catatan: Nilai yang diperoleh dianggap memenuhi bila dalam interval .
Kemungkinan 2:
Untuk nilai tertentu, kita peroleh nilai .
Jadi, himpunan penyelesaian untuk nilai adalah .
D.Nilai
yang memenuhi persamaan untuk adalahDiketahui:
Kemungkinan 1:
Untuk , diperoleh
Untuk , diperoleh
Kemungkinan 2:
Untuk , diperoleh
Untuk , diperoleh
Untuk , diperoleh
Jadi, nilai yang memenuhi persamaan tersebut bila dinyatakan dalam notasi himpunan adalah
Kemungkinan 1:
Untuk , diperoleh
Untuk , diperoleh
Kemungkinan 2:
Untuk , diperoleh
Untuk , diperoleh
Untuk , diperoleh
Jadi, nilai yang memenuhi persamaan tersebut bila dinyatakan dalam notasi himpunan adalah
5.Grafik Trigonometri

A.Diketahui grafik fungsi y1=5sinx dan y2=sin5x. Pernyataan berikut yang benar adalah
Bentuk umum fungsi sinus tersebut adalah .
Periode:
Periode dengan adalah , sedangkan periode dengan adalah .
Dapat disimpulkan bahwa periode sama dengan 5 kali periode .
Amplitudo:
Amplitudo dengan adalah , sedangkan amplitudo dengan adalah . Dapat disimpulkan bahwa amplitudo 5 kali amplitudo .
Periode:
Periode dengan adalah , sedangkan periode dengan adalah .
Dapat disimpulkan bahwa periode sama dengan 5 kali periode .
Amplitudo:
Amplitudo dengan adalah , sedangkan amplitudo dengan adalah . Dapat disimpulkan bahwa amplitudo 5 kali amplitudo .
B.Grafik memotong sumbu- di titik berkoordinat...
Apabila grafik memotong sumbu-, maka nilai . Dengan demikian,
Nilai yang membuat bernilai 0 adalah .
Jadi, titik potong grafiknya berkoordinat
Nilai yang membuat bernilai 0 adalah .
Jadi, titik potong grafiknya berkoordinat
C.Grafik di atas adalah grafik fungsi

Perhatikan sketsa gambar berikut.
Grafik di atas merupakan modifikasi grafik cosinus (karena grafiknya dimulai dari sumbu-) dengan bentuk umum .
Grafik juga menunjukkan bahwa nilai maksimum fungsinya , sedangkan nilai minimumnya , sehingga
Saat , nilai fungsinya , lalu berulang kembali di , sehingga periodenya . Dengan demikian, .
Jadi, grafik fungsi di atas adalah grafik fungsi
D.Diketahui
dengan . Daerah hasil fungsi adalahAgar mencapai maksimum, maka haruslah sebesar-besarnya, yaitu . Untuk itu,
Agar mencapai minimum, maka haruslah sekecil-kecilnya, yaitu . Untuk itu,
Jadi, daerah hasil fungsi adalah semua nilai (bilangan real) dari sampai , atau secara matematis ditulis
Agar mencapai minimum, maka haruslah sekecil-kecilnya, yaitu . Untuk itu,
Jadi, daerah hasil fungsi adalah semua nilai (bilangan real) dari sampai , atau secara matematis ditulis





mantapp, isinya bagussssssss
ReplyDeleteMANTAP GANN
ReplyDelete